论文链接
写在前面
这篇文章是光场相机标定(Light Field Camera Calibration)的经典。对光场相机的基础知识介绍较为详尽,方便快速入门。所提出的方法也已经历过生产实践的检验。
Abstract
开头是一段对光场相机应用的背景介绍,这里直接略过。
想实现深度估计就必须做相机标定(Camera Calibration)。本文提出了一个稳健的、自动化的相机标定技术。
Introduction
第一段简要介绍了一下光场相机的发展历程。
第二段提到Raytrix以“虚深度”(Virtual Depth)的形式提供物到相机的距离。并且引用10详细讲解了Raytrix相机。虚深度的概念会在后面图解,你可以暂时把它理解为一个变量与另一个随相机型号变化的常量的比值。
第三、四段简要介绍了先前提出的光场标定算法。
第五段,作者声明这个新提出的标定算法更精确地建模了MLA(Micro Lens Array,微透镜阵列),由此不仅可以更准确地度量三维空间,更可以减少深度图中的噪声。
倒数第二段提到,这篇期刊论文是先前一篇会议论文14的改进版——作者新引入了主透镜偏斜、偏移情况下的建模。
最后一段介绍文章结构。
Theoretical Foundations
这一大章都在讲理论基础。因为我也刚入门,所以就除了实验结果外全篇翻译一下。
Depth estimation
下图是Plenoptic 2.0(聚焦式全光相机)的成像示意图。
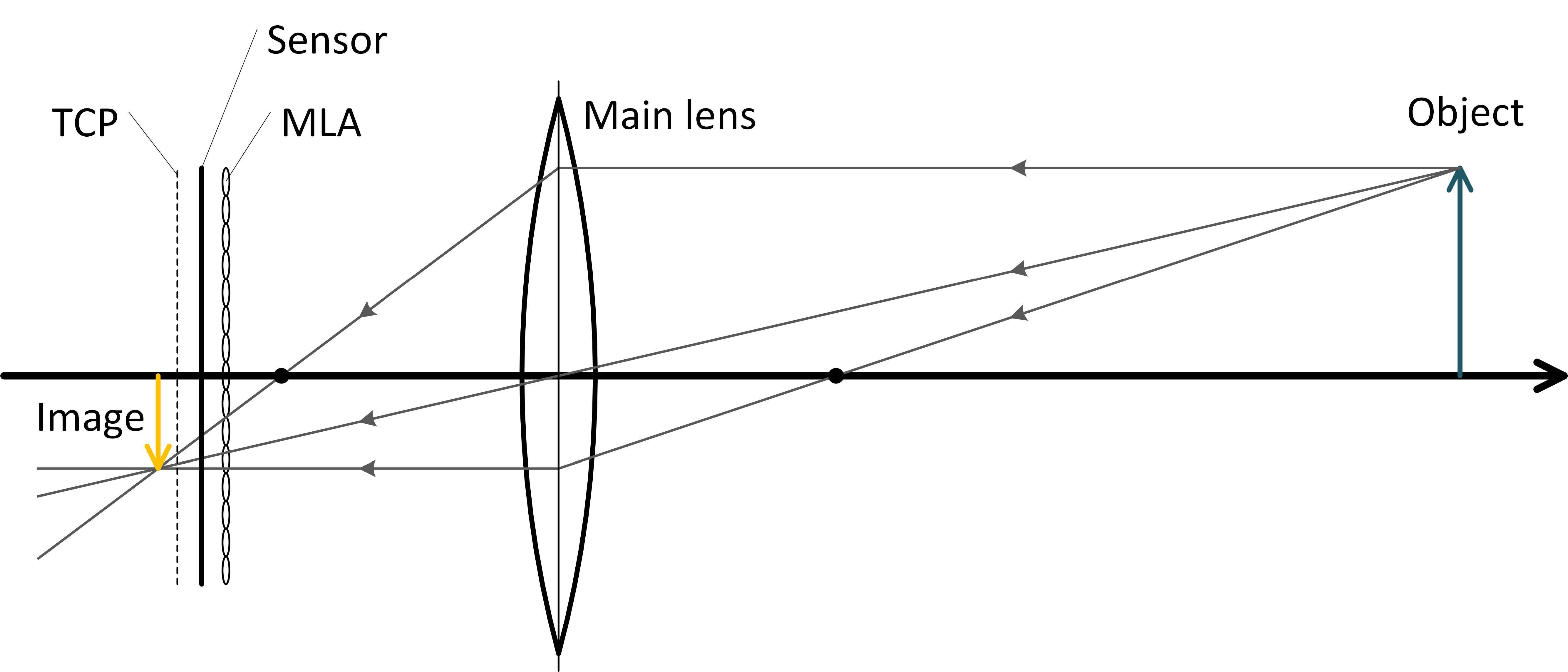
上图中,Image是仅有主透镜无MLA的成像位置。MLA将光线会聚的位置“提前”到了TCP(Total Covering Plane,不知道怎么翻译)所在的位置。我们在MLA之后,TCP的附近放置传感器,这样每个ML都会在传感器上成一个小圆像。这些小圆像被称作MI(Microlens Image)。相邻的MI存在部分相似,这是因为物体上同一块区域发出的光可以由紧邻的多个ML成像,相邻的MI包含了物上的同一区域,自然也就存在相似性了。我们可以进一步利用这些相似区域之间的距离关系估算深度。
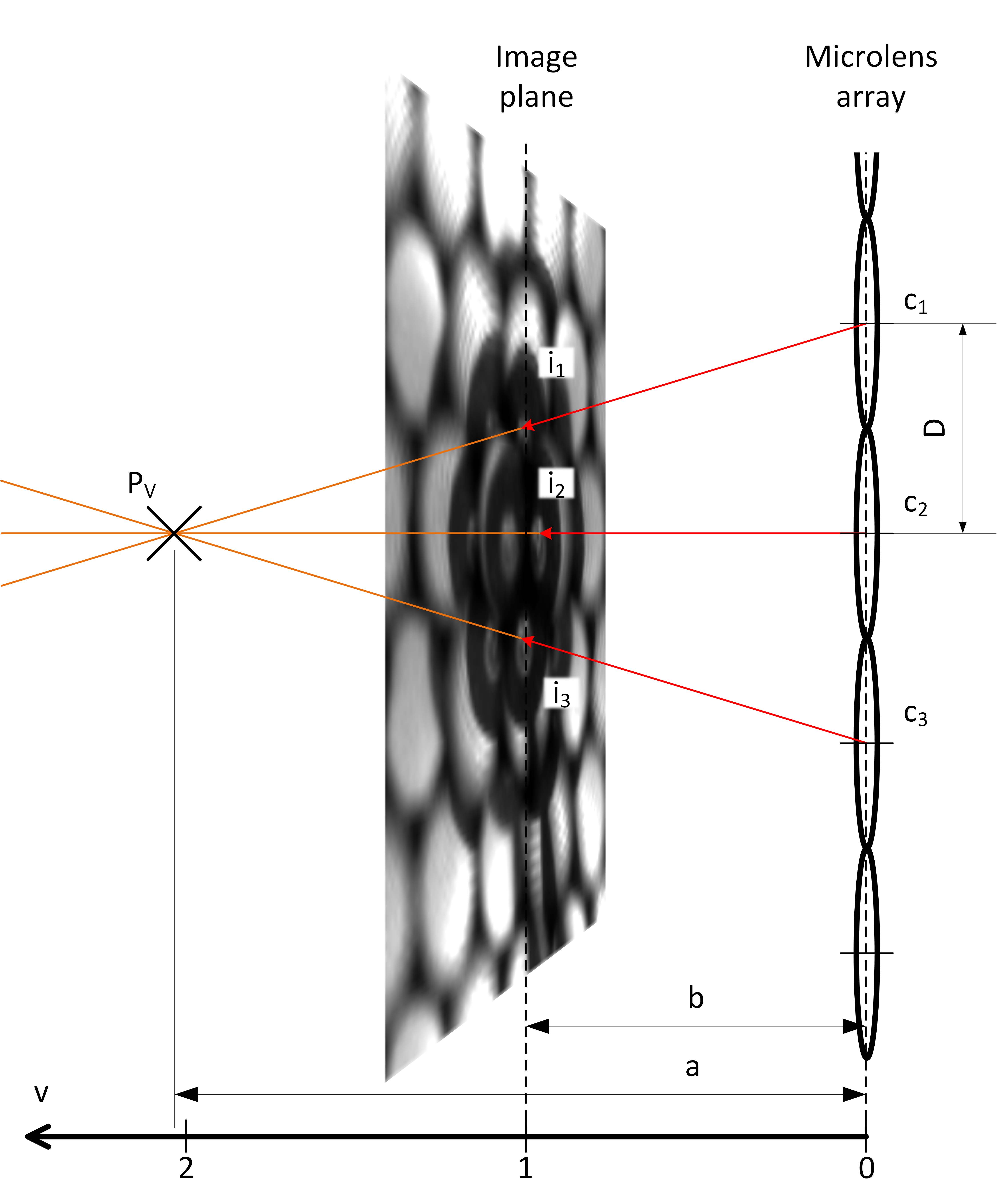
如上图所示,由物上一点发出的三条特殊光线,恰好经过三个ML(Micro Len,微透镜)的中心点,打在成像平面上的i1、i2和i3三点,最终会聚于PV点。因为光线恰好穿过ML中心,因此并未发生偏折,PV其实就是主透镜的焦点。而所谓成像平面其实就是ML的焦平面。中三个ML的中心点分别记作c1、c2和c3。图中的D是相邻ML的中心距离。a是PV点“到相机的距离”a,也就是到MLA主平面的距离。b是成像平面(注意成像平面≠传感器)到MLA主平面的距离,并且是一个常量,但我们通常并不能直接得知,所谓标定,终极目标就是把这个b标定出来。
计算b之前要先计算PV点的虚深度v。虚深度的计算公式如下:
$$v = \frac{a}{b} = \frac{D}{D-(i_1-i_2)}$$
Raytrix相机还有一个多焦点(Multi-Focus)的特性,即在相机的MLA中存在三种不同焦距的ML。该特性使得相机能获得更大的景深(DoF,Depth of Field),但也会造成一种特殊的“偏差”(aberration),如下图所示,即测量出三种不同的成像平面。
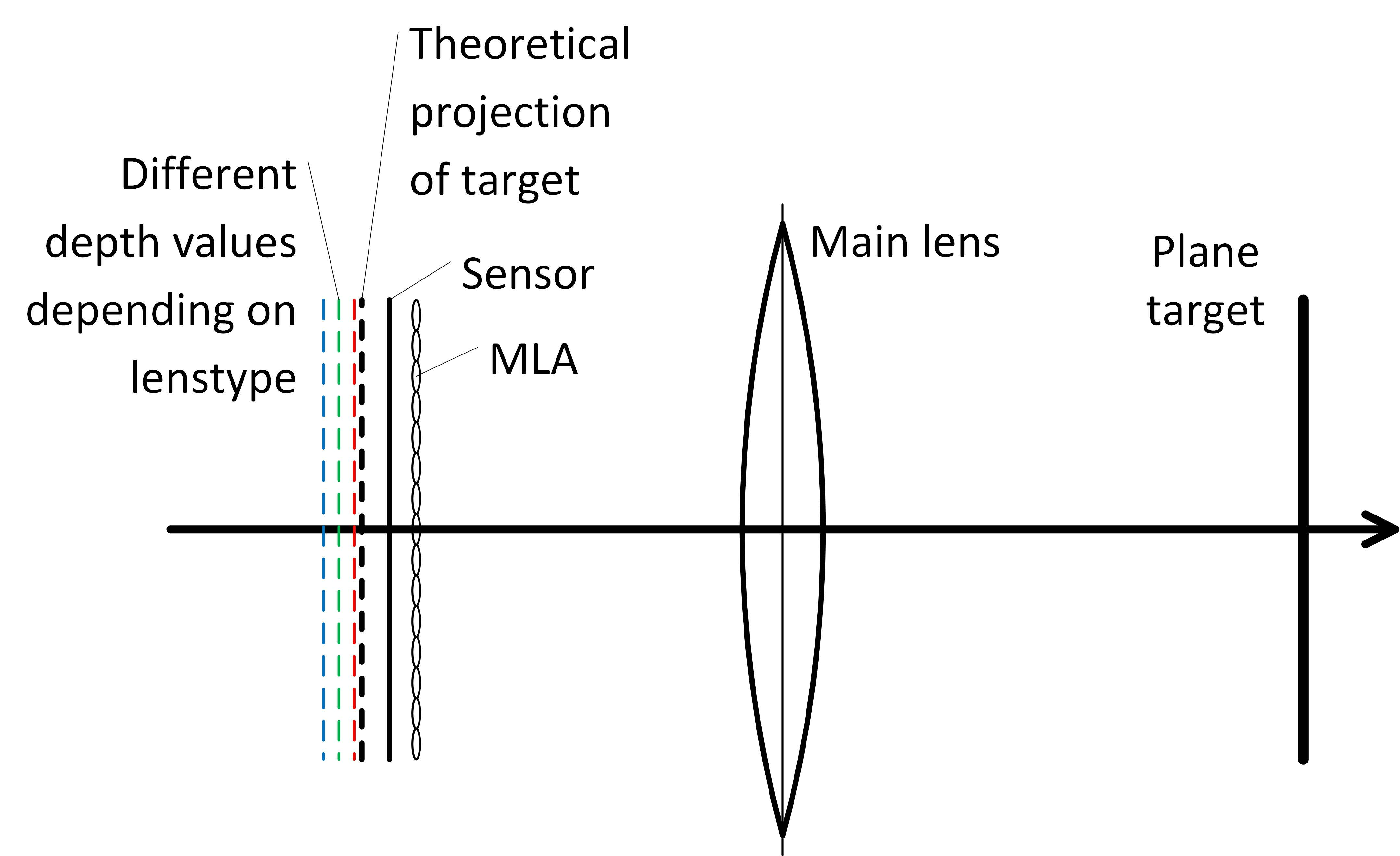
因为成像平面到MLA主平面的距离与虚深度线性相关,由此我们可以假定对不同的ML有不同的b,并用bi表示第i种ML对应的b。
Projection model
下图粗略地演示了从MLA左侧的虚深度到主透镜右侧的真实深度的转换过程。该图同样展示了投影过程中各个空间的名称。
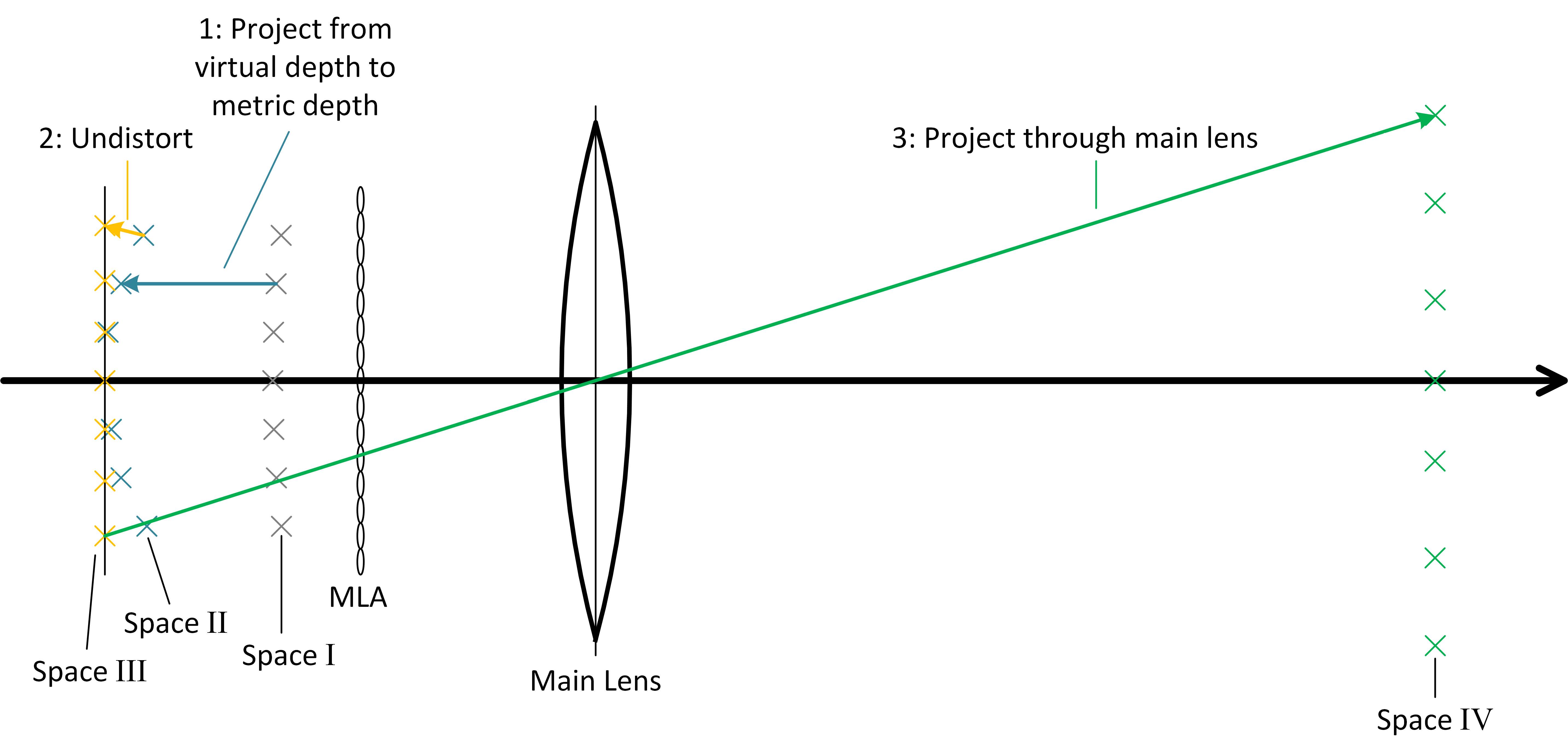
空间Ⅰ中的点由“横向”(这里指的是垂直于主光轴的方向,搞不懂为什么要叫lateral)的坐标再加上虚深度来表示。空间Ⅱ中的点是由空间Ⅰ投影而来的真实坐标,其实就对应了PV的坐标。空间Ⅲ的点为去变形(undistorted)之后的点。去变形的效果就相当于把主透镜摆正。空间Ⅳ的点为对应的真实物体上的点,也反映了真实深度。这些点的x、y坐标轴与主光轴垂直,z坐标轴与主光轴平行。感觉原始概念有些难以理解,还是来看公式吧。
由于虚深度对应了空间Ⅰ中的坐标(x,y,z)Ⅰ,因此我们可以利用公式$v = \frac{a}{b_i}$投影得到空间Ⅱ中的坐标(x,y,z)Ⅱ:
xⅡ = xⅠ ⋅ bi yⅡ = yⅠ ⋅ bi zⅡ = zⅠ ⋅ bi
然后是从空间Ⅱ到空间Ⅲ的去变形步骤。这里的变形由主透镜的倾斜(Tilt)和偏移(Shift)导致。需要注意的是,主透镜倾斜和偏移产生的变形效果各自独立。作者这里使用了来自引用15(Decentering distortion of lenses,作者Brown,我没找到原文)的方法来解决偏移变形;而倾斜变形可以通过简单的旋转变换纠正。
为建模主透镜在倾斜和偏移状态下的3D位姿,以下定义一系列变量。θL、σL用于表示主透镜的朝向角;XL、YL用于表示主透镜中心相对传感器中心的坐标偏移;而主透镜与传感器之间的距离被定义为ZL。这个ZL不需要特意求取,因为我们后面的计算只会用到主透镜与TCP之间的距离BL。变量的可视化如下图所示:
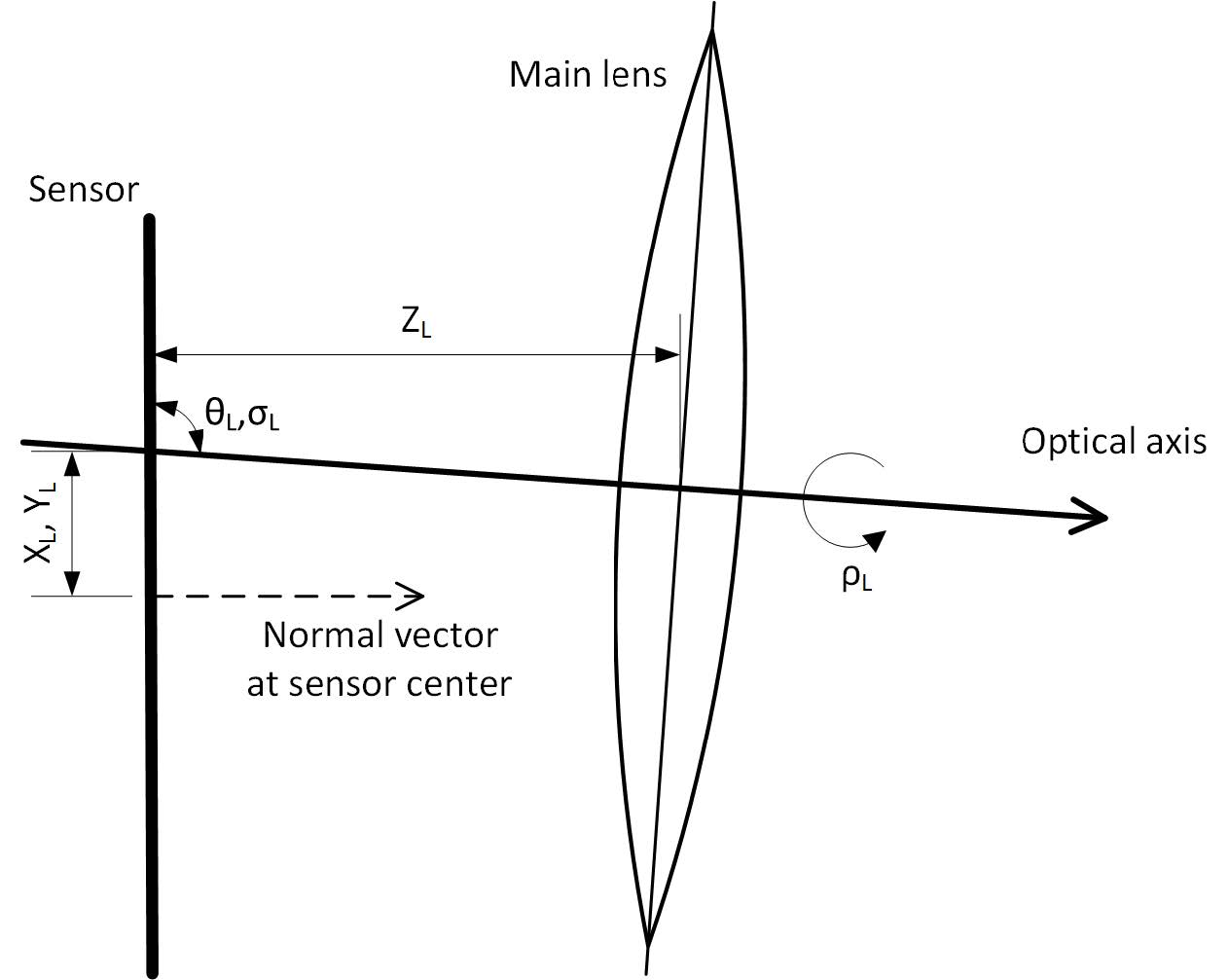
对于光场相机而言,主透镜的倾斜会导致最终成像的倾斜,如下图所示。这一效应被称为沙姆定律(Scheimpflug Principle)。关于沙姆定律的一些科普可以看这篇知乎文章《移轴摄影、沙姆定律与射影几何》。
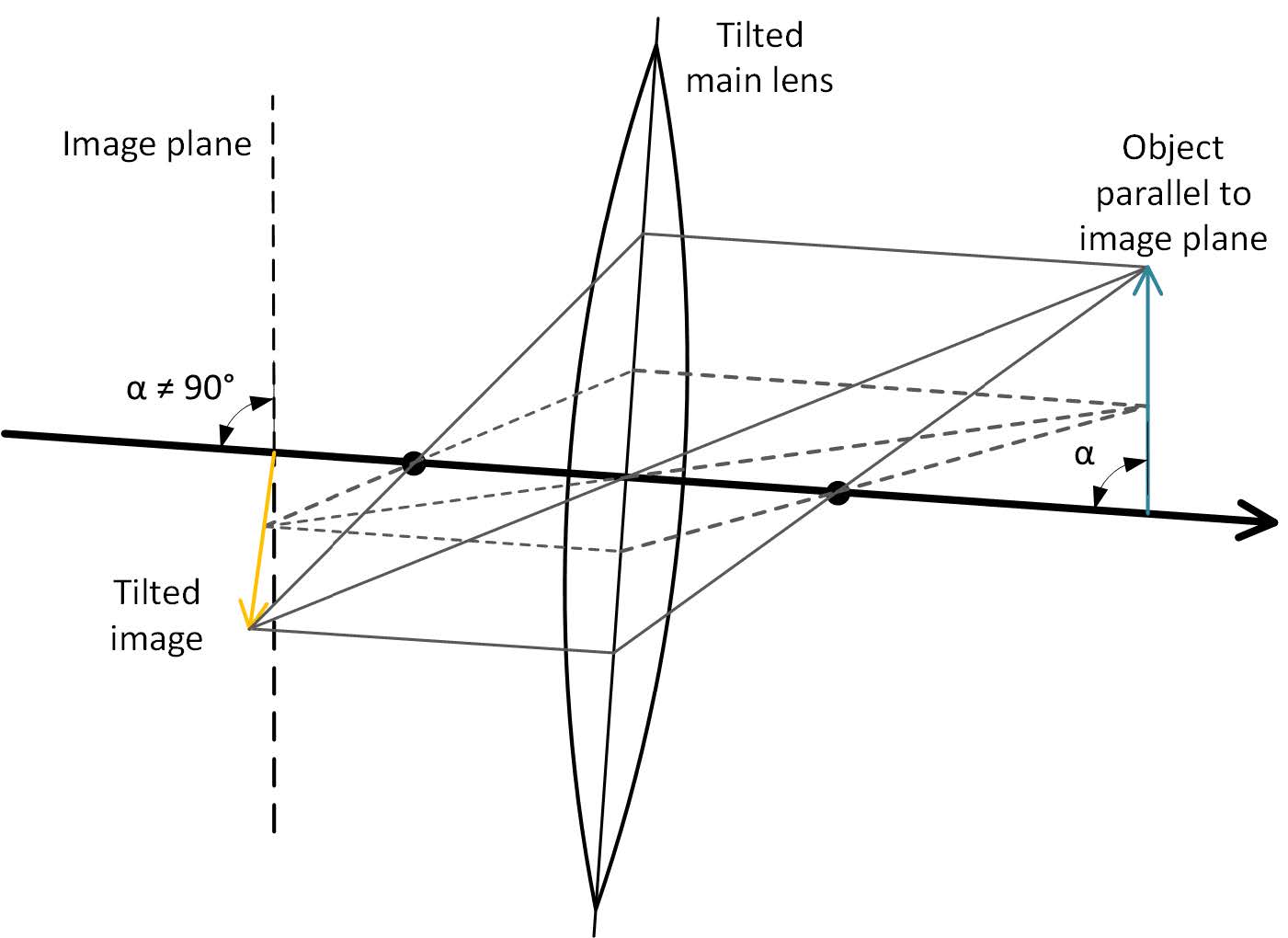
以沙姆定律为基础,我们可以通过一次旋转来纠正倾斜变形。这次旋转的旋转轴应与主光轴垂直。
接下来我们使用引用15的方法来解决偏移变形。其作者Brown认为变形量由两个变形系数k1、k2定义。由空间Ⅱ到空间Ⅲ的x、y坐标转换公式如下:
xⅢ = xⅡ ⋅ (1+k1r2+k2r4) yⅢ = yⅡ ⋅ (1+k1r2+k2r4)
其中r表示空间Ⅱ中的点到“变形中心”(distortion center,主光轴与传感器平面的交点)的欧氏距离(坐标平方和开方)。
然后我们需要做径向深度去变形(radial depth undistortion)。这部分的变形量由与r绑定的系数d1、d2,以及与虚深度zd(不明白这里为什么不用vd)绑定的系数dd定义。其中虚深度对变形量的增益是线性的。这一步去变形对应的公式如下:
zⅢ′ = zⅡ + (1+zddd) ⋅ (d1r2+d2r4)
注意zⅢ′度量的是到MLA的距离,而空间Ⅲ中的距离应当从主透镜的主平面起算。为了获得“真正的”zⅢ,首先计算主透镜与TCP之间的距离BL:
$$B_L = \frac{T_L}{2} \left( 1 - \sqrt{1 - 4 \frac{f_L}{T_L}} \right)$$
其中fL是主透镜的焦距,TL为主透镜的对焦距离(焦点到被摄物体的距离?)。这里各种距离的概念有点多,为方便读者理解我把上面的那张成像示意图再贴一遍。

现在,只需要把从MLA起算的深度zⅢ′与主透镜到TCP的距离BL加起来,再减去MLA到TCP的距离就能得到从主透镜起算的深度,亦即空间Ⅲ中的深度zⅢ了。而根据光场相机的设计理论,TCP到传感器的距离恰好等于传感器与MLA之间的间距bi(bi不是随透镜类型变化的吗?而传感器与MLA之间的间距似乎是个固定值?这里我没读懂。)。于是我们可以写出zⅢ的表达式:
zⅢ = zⅢ′ + BL − 2bi
最后使用薄透镜理论
$$\frac{1}{f_L} = \frac{1}{G_L} + \frac{1}{B_L}$$
将zⅢ投影到物方的空间Ⅳ中即可。
Implementation
这章主要讲光场相机标定算法的实现,以及标定参照物的设计。对于传统相机的标定,棋盘格是常用的参照物。但对于光场相机,当棋盘格的边界与对极线(epipolar lines)平行时将无法估计深度。换用圆形图案的参照物可以解决这一问题。
我们使用MSER算法来从图像中提取圆形图案特征。随后使用引用18(Design and test of a calibration method for the calculation of metrical range values for 3D light field cameras,一篇硕士学位论文,找不到链接)中给出的算法将特征点对齐到网格并将相邻特征点的像素间距关联到真实距离。
在这之后,我们获得了两组点集,第一组是从拍摄图像中提取的,与虚深度关联的目标点集(target points);第二组是对齐到间距已知的矩形网格的模型点集(model points)。并且两组点之间存在一一对应的关系。利用这一关系我们便能完成对相机内参(intrinsic parameters,也称固有参数)的优化。
利用上一章中提到的方法,使用一组初始内参将目标点集投影到空间Ⅳ中。如果内参取值恰当,那么投影后的目标点应当与其实际所在的位置重合。而这一实际位置可由zⅣ = 0平面上的模型点集经过一仿射变换表示。为计算归一化的损失,不妨对目标点集施加一个仿射逆变换,使其变换到zⅣ = 0平面上,再利用变换后的目标点与模型点之间的距离来计算归一化损失。
最后一段大意是提供的样本越多,用于优化参数的方程组就越超定,所以这套标定算法是相当健壮的。